
USER'S MANUAL
Written by Vladimir Támara Patiño.
2001
CONTENTS

|
|
1.2. References |
|---|---|
|
|
|
|
|
|
| 4. THE MANTA SYSTEM | 4.1 The interfaces
4.2 Types 4.3 Theorem Prover and rewriting motor 4.4 Generation of Code |
|
|
|
Some portions of the source code and documentation of ManTa are covered by the GPL, other parts belong to the public domain.
The code generated by ManTa has not copyright restrictions, the copy conditions can be imposed freely by the author of the ManTa specification, that originated the code.
[Tor91] TORO, Victor Manuel. Organización y documentación de programas grandes en C (ANSI), Memo de investigación 52, Circulación privada Centro de Documentación de la Facultad de Ingeniería de la Universidad de los Andes, 1991.
If you download a binary distribution, just install it (after decompressing it, if necessary). The sources can be compiled in several variants of Unix (e.g Linux, SunOS, OpenBSD) as well as in DOS like systems (e.g Windows 95, Windows NT, DOS of 32bits --even without long name support). The precise instructions to compile them can be found along with the sources in the file INSTALL, here we present only a table that summarizes the features of ManTa in each type of platform:
| Feature | Unix | Dos |
|---|---|---|
| I. Distribution | ||
| Preferred dist. | sources | binaries |
| II. Compilation and tailoring of sources | ||
| Configuration method | configure | edit makefile.dj |
| Compilation | gcc,make,sed | gcc (djggp), make, sed |
| Binaries (*) | /usr/local/bin | /manta/ |
| Shared data (*) | /usr/local/share/manta | /manta/ |
| Elisp data (*) | /usr/local/share/emacs/site-lisp | /manta/ |
| Documentation (*) | /usr/local/share/doc/manta | /manta/ |
| User directory | ~/.manta | /manta/ |
| III. Final Binaries | ||
| Configuration by final users | manconf | manconf |
| Support several users | Yes | No |
| Interfaces supported | Command line, plain, emacs | Command line, plain, emacs |
| Support for several languages | Yes | Yes |
| Compilers supported | gcc or cc, any make | gcc (djgpp or cygnus), bcc any make |
(*) In Unix the exact prefix can be configured in the configuration step (it doesn't have to be `/usr/local'); what we want to emphasize here is that in dos, all the directories coincide while in unix they can be in different locations (for example to enable multiple users or to share data in a network).
manconfmanconf allows the user to choose: the language of the interface, a text editor (that will be used for editing ADTs, sources or displaying some information) and a compiler (that will be used to compile the generated code).
By editing the appropriate configuration files, other aspects of ManTa can be configured:
By default the plain interface, with standard directories, messages, labels and templates will be configured by manconf, if you want to use the emacs interface, check the instructions in the file readme.txt of the documentation directory (you can check the path of the documentation directory by running manconf).
To configure more fine details edit the appropriate configuration files. All the configuration files have a similar format: text files, where each line could have a line number followed by a space, a configuration option between dots (e.g.: ".D_ADT.") and after that commentaries (the commentaries cannot include dots).
.<Emacs interface>. 0 if you want plain interface, 1 if you want Emacs interface .<editor>. Name of the text editor to use (when using plain interface). If blank the standard input will be used .<option1>. Command line option of the editor to go to a specific line .<option2>. Command line option of the editor to edit a file in read only mode .<dir_messages>. Directory with messages of the systems .<dir_templates>. Directory with templates for C code .<dir_adts>. Directory to save bytecode of ADT .<dir_temp>. Directory to save temporary files. .<dir_print>. Directory to save "printed" TADs (i.e textual representation) .<unused>. .<dir_conj>. Directory to save conjectures and theorems .<dir_prot>. Directory to save generated code .<unused>. .<file_keywords>. Name of keywords file (it must be in directory <dir_messages>) .<file_menus>. Name of file with menus lables (it must be in <dir_messages>) .<file_messages>. Name of file with messages (it must be in <dir_messages>) .<header_func.i>. Template for function header (must be in <dir_templates>) .<tad.c>. Template for selectors (must be in <dir_templates>)
.<tad.h>. Template for headers .<tad.mak>. Template for makefile .<tad_cons.inc>. Template for constructors .<tad_defs.h>. Template for data declaration .<tad_inter.c>. Template for interface functions .<tad_inter.h>. Template for header of interface functions .<tad_main.c>. Template for the main program
<number> .<message>.
Where the number is the internal code for the message, a space is required after the number, and dots before and after the message are also required. The message can contain control characters like \n, \t, %d, %s (typical for printing strings with the function printf in ANSI C).
ManTa is distributed with two messages files, they are located in the directory for messages (see the previous section).
In the directory for templates there are available versions of these templates in spanish and in english
The ManTa system consists of a kernel and an interface. The
interface can be changed in accordance to your needs, now there are availabe three interfaces: command line tools, a plain (text) interface and an interface for the emacs text editor. The kernel of ManTa has three major components, that will be presented in this section along with the interfaces:
mantaoptionally you can pass as options:
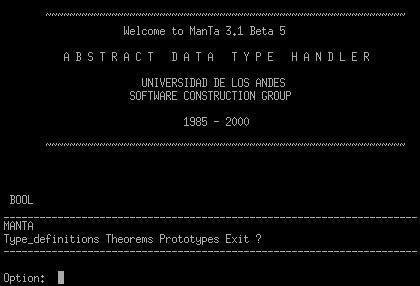
All the interaction with this interface is done through menus. You can choose the desired option by typing it or part of it and then pressing ENTER. In all the menus there is an option Exit to return to the previous menu (in the case of the top menu, it will exit from the program), pressing ENTER without a word is equivalent to choose Exit.
There are many operations that require edition of texts, this edition
is done with an external text editor, that must be configured as explained
in section 2.
Once configured, run the Emacs editor (e.g. emacs).
Press C-c m (i.e. [CTRL]+[C] and then [M]). In the status bar should
appear "Configuration file for ManTa:", press [ENTER] and you will
see the Main Menu.
To choose an option put the cursor on it, and press [ENTER].
.

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
There are two important implementation details to have in mind:
New ADTs can be created from scratch, by using the ManTa language
or can be created semi-automatically with metaoperations. A
brief description of the ManTa language and of the metaoperations will
be given. A complete description including semantics issues can be found
in [LangSpec].
Given one or more ADTs, it is possible to specify operations on it/them. These operations are specified with functions called here selectors. The selectors are intended to be functions that receive a value from a given domain and produce a value in a codomain. In ManTa the domain can be an ADT or the cartesian product of ADTs and the codomain must be an ADT. For example the function AND: BOOL * BOOL -> BOOL, expects two booleans and produce a third boolean.
Every ADT in ManTa has two sections: signature and axioms. In the signature the generators and the selector of the ADT are presented, including its type (i.e. domain and codomain) and other abstract information. In the axioms section the behavior of each function is described. The syntax of an ADT in ManTa is:
ADT name [parameter]
INITIALS
initials
CONSTRUCTORS
constructors
SELECTORS
selectors
AXIOMS
axioms
The signature is composed by the initials, the constructors and the selectors. The name of the ADT must be a string (without special characters). The parameter (a type place holder) is optional and when it appears the type is generic or parametric.
The initials are generators of the ADT whose domain doesn't contain the defined ADT (in particular constants are initials), the constructors are generators of the ADT that must include in its domain the defined ADT. For example in accordance to Peano, the natural numbers can be produced with the constant 0 and the successor function. In ManTa it is represented with the ADT NAT that has as generators the initial ZERO:->NAT and the constructor SUC:NAT->NAT
The axioms of an ADT specify the behavior of the selectors, this behavior
must be specified with several restrictions, those restrictions make the
description sometimes difficult, but they ensure many theoretical aspects
(for example that what you write has a logical model, that you will be
able to state conjectures easily, that it can be translated to several
languages, and that the selectors are conservative). Each axiom must be
of the form:
leftside=rightside
The leftside must
be a selector instatiated with generators and variables (no repeated variables),
the right side can be an expression like :
PRED(ZERO)=ERRORNote that x is a variable, and ERROR was used to specify that the PRED function is undefined in ZERO.
PRED(SUC(x))=x
Other requirements that the specifications must fulfill are (checked by the system, before accepting a new ADT): everything must have type, the axioms for a selector must cover the domain, the axioms for a selector must be strongly locally confluent (this last property ensures that there are no contradictions between two axioms for the same selector).
It's a good moment to check the whole specification of the ADTs BOOL and NAT that appears in the Apendix A of this manual.
Note that those types (NAT and BOOL) as well as any other basical type, must have an equality. The name of the equality must be EQ_name where name is the name of the ADT. A basical type is a specification with generators and without parameters; when a specification doesn't have generators, it does not represent a set but it must have selectors that operate with existing ADTs. These specifications are called extensions and they don't need an equality, as the following example shows:
ADT ExtNAT[]An ADT with a parameter is a generic type (also known as parametric type), these types can be instantiated, that is its parameter can be replaced with an existing type to produce a new type. By now a generic types can have at most one parameter. One example of a generic ADT can be found in the Apendix A, the classical ADT List[X].
INITIALS
CONSTRUCTORS
SELECTORS
ack: NAT(i) * NAT -> NAT
/* Ackerman function, this shows that ManTa can express more than
primitive recursive functions */AXIOMS
ack(ZERO,y)=SUC(y)
ack(SUC(x),y)=
if ISZERO(y) then
ack(x,SUC(ZERO))
else
ack(x,ack(SUC(x),PRED(y)))
fi
It is also possible to write a generic extension, although with this
technique by now, probably the only interesting example is:
ADT AddNEQ [T]
/* When this type is instantiated an extension to type T is produced. T is extended with a not-equal predicate */INITIALS
CONSTRUCTORS
SELECTORS
NEQ: T*T->BOOL
AXIOMS
NEQ(x,y)=NOT(EQUAL(x,y))
As a summary the following table describes a classification of types
in ManTa:
| Name | Generators | Parameters | Commentaries |
| Basic Type |
|
Usual ADT (e.g. NAT) | |
| Extension | They only add new selectors to the system of ADTs | ||
| Generic Type |
|
|
Also known as parametric types (e.g. List). |
| Generic Extension |
|
Types that generate extensions when instanced |
In addition to this classification, basic ADTs can be:
From the computability point of view, considering the selectors, any primitive recursive function can be expressed, but also non primitive recursive functions like the Ackerman functions can be easily written. It is also possible to write a simulator for a Turing machine in ManTa, hence ManTa can compute any Turing-computable function.
From the set theoretic point of view, the problem of the sets that can
be represented is more delicate, since in ManTa they must be produced by
generators (initials and constructors), and there is no way to express
restrictions on the generators.
By a moment let's avoid the equality function and let's suppose that
for all ADTs it is the syntactical equality. In this case,
finite sets can be represented, but it is mandatory to write explicitly
all the elements of the set with initials (all the elements must be written
as constants, or part of them can be embedded from another finite set with
initials). If there is at least one constructor the set is infinite,
and its cardinality cannot be greater than w (cardinality of natural numbers).
The introduction of the equality generates equivalence classes in the represented
set, and hence it cardinality decreases or remains equal.
Since it's also possible to write mutually recursive types (the generators of both ADTs depend on each other), the expressiveness of ManTa to generate types is the same that the Caml, C, Pascal, Java or any typical programming language. However some languages give more help to write finite sets (for example in Pascal an interval can be written as a..b). In ManTa this effect cannot be achieved although the mechanism of restriction can help in such situation.
From the logical point of view the question "What can be proved?"
is more interesting. By now the theorem prover of ManTa only has support
for universally quantified equalities, and it assumes that the variables
always take defined values.
| Operation | Input | Output | Typical Example | User intervention |
| Instatiation | A generic type and a basic type | A new type obtained after instatiation of the parameter in the generic type with the basic one. | Instantiate List[X] with NAT to obtain a list of natural numbers | No |
| Copy | Any type/extension | A new type/extension with names changed | Copy NAT as NAT2 (all the function names will be changed) | No |
| Cartesian Product | Two basical types | The cartesian product of the inputs with some additional selectors | NAT x NAT two obtain a TAD of pairs of Naturals | No |
| Restriction | A basical type and a restriction predicate that must be defined for all the type | An extension to the type with analogous function but defined only where the predicate is TRUE | NAT restricted to the predicate EvenNAT to obtain functions that operate only on Even naturals | No |
| Direct Sum | Two different basical types | Union between the input types. | Defines all the selectors (of both types) for the new generators | |
| Completation | A basical type and a new symbol | A new type with analogous generators to the received type plus the new symbol as a new constant of the type | Complete NAT with a new symbol INF to represent Infinite. | Redefine all the selectors in the new constant |
| Variation | Two basical types | A new type that can be seen as the first or as the second | Complex numbers in polar notation and Complex numbers in cartesian notation with a variation to yield Complex numbers. | The user must give functions to translate from one representation to the other and optionally can add new operations on both. |
| Representation | Two basical types | A new extension of the second type to "codify" the functionality of the first | BOOL represented with NAT (for example TRUE with ONE and FALSE with ZERO) | The user must specify all the selectors of the represented type. The system generates prove obligations (see sec. ) |
| Composition of Representations | Two representations "compatible" | A new representation obtained by composition | BOOL represented with NAT, NAT represented with Lists of one symbol, to obtain BOOL represented with Lists of one symbol. | No |
The mentioned examples are now shown in more detail, however not the whole ADT is transcribed in all the cases, just some portions of each one. (You can see the whole example by using the ManTa system!)
Instatiation. The parameter X of List
is instanced with NAT to produce type ListNAT:
ADT ListNAT [ ]INITIALS
nil_ListNAT : -> ListNATCONSTRUCTORS
cons_ListNAT: NAT * ListNAT -> ListNATSELECTORS
head_ListNAT : ListNAT(i) -> NAT
tail_ListNAT : ListNAT(i) -> ListNAT
length_ListNAT : ListNAT(i) -> NAT
concat_ListNAT : ListNAT(i) * ListNAT -> ListNAT
memberList_ListNAT : ListNAT(i) * NAT -> BOOL
isEmptyList_ListNAT : ListNAT(i) -> BOOL
EQ_ListNAT(c): ListNAT(i) * ListNAT(i) -> BOOLAXIOMS
head_ListNAT(nil_ListNAT) = ERROR
head_ListNAT(cons_ListNAT(X1,L2)) = X1...
memberList_ListNAT(nil_ListNAT,X1) = FALSE
memberList_ListNAT(cons_ListNAT(X1,L2),X3) = if EQ_NAT(X1,X3)
then TRUE
else
memberList_ListNAT(L2,X3)
fi
...
Copy. The ADT NAT has been copied in
NAT2
ADT NAT2 [ ]INITIALS
ZERO_NAT2 : -> NAT2CONSTRUCTORS
SUC_NAT2 : NAT2 -> NAT2SELECTORS
ADD_NAT2 : NAT2 * NAT2(i) -> NAT2
ISZERO_NAT2 : NAT2(i) -> BOOL
...AXIOMS
ADD_NAT2(N1,ZERO_NAT2) = N1
ADD_NAT2(N1,SUC_NAT2(N2)) = SUC_NAT2(ADD_NAT2(N1,N2))ISZERO_NAT2(ZERO_NAT2) = TRUE
ISZERO_NAT2(SUC_NAT2(N1)) = FALSE...
Cartesian Product. Pair of naturals
ADT Pair [ ]
/* = NAT x NAT */INITIALS
PAIR_Pair : NAT * NAT -> PairCONSTRUCTORS
SELECTORS
PROY_Pair1 : Pair(i) -> NAT
PROY_Pair2 : Pair(i) -> NAT
SUC1 : Pair -> Pair
ADD_Pair1 : Pair * Pair(i) -> Pair
...
SUC2 : Pair -> Pair
ADD_Pair2 : Pair * Pair(i) -> Pair
ISZERO_Pair2 : Pair(i) -> BOOL
...AXIOMS
PROY_Pair1(PAIR_Pair(N1,N2)) = N1
PROY_Pair2(PAIR_Pair(N1,N2)) = N2
SUC1(P1) = PAIR_Pair(SUC(PROY_Pair1(P1)),PROY_Pair2(P1))
ADD_Pair1(P1,P2) = PAIR_Pair(ADD(PROY_Pair1(P1),PROY_Pair1(P2)),PROY_Pair2(P1))
Restriction. The ADT NAT restricted to the predicate EvenNAT:NAT->BOOL given by
ADT ENAT [ ]
/* = ( NAT : EvenNAT )*/INITIALS
CONSTRUCTORS
SELECTORS
EvenNAT (c): NAT(i) -> BOOL
ADD_ENAT : NAT * NAT -> NAT
ISZERO_ENAT : NAT -> BOOL
...AXIOMS
EvenNAT(ZERO) = TRUE
EvenNAT(SUC(N2)) = NOT(EvenNAT(N2))ADD_ENAT(X1,X2) = if AND(EvenNAT(X1),EvenNAT(X2))
then ADD(X1,X2)
else ERROR
fiISZERO_ENAT(X1) = if EvenNAT(X1)
then ISZERO(X1)
else ERROR
fi
...
Direct Sum.
Completation. A possible completion of NAT with
a symbol for infinite i.e INF.
ADT INAT [ ]
/* = NAT + { INF }*/INITIALS
ZERO_INAT : -> INAT
INF : -> INATCONSTRUCTORS
SUC_INAT : INAT -> INATSELECTORS
ADD_INAT : INAT * INAT(i) -> INAT
ISZERO_INAT : INAT(i) -> BOOL
...AXIOMS
ADD_INAT(N1,ZERO_INAT) = N1
ADD_INAT(N1,SUC_INAT(N2)) = SUC_INAT(ADD_INAT(N1,N2))
ADD_INAT(N1,INF) = INFISZERO_INAT(ZERO_INAT) = TRUE
ISZERO_INAT(SUC_INAT(N1)) = FALSE
ISZERO_INAT(INF) = FALSE
...
Variation. The ADT ComplexPol (complex in
polar representation) along with the ADT ComplexCart (complex
in cartesian representation) can be viewed as one, via the variation Complex
ADT Complex [ ]
/* = ComplexPol U ComplexCar */INITIALS
Complex_ComplexPol: ComplexPol -> Complex
Complex_ComplexCar: ComplexCar -> ComplexCONSTRUCTORS
SELECTORS
ComplexPol_ComplexCar : ComplexPol(i) -> ComplexCar
ComplexCar_ComplexPol : ComplexCar(i) -> ComplexPol
EQ_Complex(c): Complex(i) * Complex(i) -> BOOLAXIOMS
...
EQ_Complex(Complex_ComplexPol(C1),Complex_ComplexPol(C2)) = EQ_ComplexPol(C1,C2)
EQ_Complex(Complex_ComplexPol(C1),Complex_ComplexCar(C2)) = EQ_ComplexCar(ComplexPol_ComplexCar(C1),C2)
EQ_Complex(Complex_ComplexCar(C1),Complex_ComplexPol(C2)) = EQ_ComplexCar(C1,ComplexPol_ComplexCar(C2))
EQ_Complex(Complex_ComplexCar(C1),Complex_ComplexCar(C2)) = EQ_ComplexCar(C1,C2)
Representation. BOOL represented with NAT
in an extension called BOOLN
ADT BOOLN [ ]
/* BOOLN : BOOL -> NAT */INITIALS
CONSTRUCTORS
SELECTORS
BOOLN_TRUE : -> NAT
BOOLN_FALSE : -> NAT
BOOLN_AND : NAT * NAT -> NAT
BOOLN_OR : NAT * NAT -> NAT
BOOLN_NOT : NAT -> NAT
BOOLN_IMP : NAT * NAT -> NAT
BOOLN_EQ_BOOL : NAT * NAT -> BOOLAXIOMS
BOOLN_TRUE = SUC(ZERO)
BOOLN_FALSE = ZERO
BOOLN_AND(N1,N2) = MULT(N1,N2)
BOOLN_OR(N1,N2) = MIN(ADD(N1,N2),SUC(ZERO))
BOOLN_NOT(N1) = MOD(SUC(N1),SUC(SUC(ZERO)))
BOOLN_IMP(N1,N2) = BOOLN_OR(BOOLN_NOT(N1),N2)
BOOLN_EQ_BOOL(N1,N2) = EQ_NAT(N1,N2)
The given representation can be proved to be correct. i.e that all
the valid axioms of selectors in BOOL are still valid.
All the axioms are valid, however with the automatic theorem prover of
ManTa, 13 of the 14 axioms can be demostrated.
Another representation will be given , here NAT will be represented with a List of Boolean (called here lb). The resulting representation is called nlb
ADT nlb [ ]INITIALS
CONSTRUCTORS
SELECTORS
nlb_ZERO : -> lb
nlb_SUC : lb -> lb
nlb_ADD : lb * lb -> lb
nlb_ISZERO : lb(i) -> BOOL
nlb_MULT : lb(i) * lb -> lb
nlb_PRED : lb -> lb
nlb_MAX : lb * lb -> lb
nlb_MIN : lb * lb -> lb
nlb_GT : lb * lb -> BOOL
nlb_LT : lb * lb -> BOOL
nlb_GE : lb * lb -> BOOL
nlb_LE : lb * lb -> BOOL
nlb_FACT : lb(i) -> lb
nlb_EXP : lb * lb (i) -> lb
nlb_EVEN : lb -> BOOL
nlb_ODD : lb -> BOOL
nlb_DIV : lb * lb -> lb
nlb_MOD : lb * lb -> lb
nlb_DIVIDES : lb * lb -> BOOL
nlb_SUBS : lb * lb -> lb
nlb_EQ_NAT : lb * lb -> BOOLAXIOMS
nlb_ZERO=nil_lb
nlb_SUC(L1)=cons_lb(TRUE,L1)
nlb_ADD(L1,L2)=concat_lb(L1,L2)
nlb_ISZERO(nil_lb)=TRUE
nlb_ISZERO(cons_lb(L1,P1))=FALSE
nlb_MULT(nil_lb,L2)=nil_lb
nlb_MULT(cons_lb(P1,L1),L2)=nlb_ADD(nlb_MULT(L1,L2),L2)
nlb_PRED(L1)=tail_lb(L1)
nlb_MAX(L1,L2)=if GT(length_lb(L1),length_lb(L2)) then L1 else L2 fi
nlb_MIN(L1,L2)=if LT(length_lb(L1),length_lb(L2)) then L1 else L2 fi
nlb_GT(L1,L2)=GT(length_lb(L1),length_lb(L2))
nlb_LT(L1,L2)=LT(length_lb(L1),length_lb(L2))
nlb_GE(L1,L2)=GE(length_lb(L1),length_lb(L2))
nlb_LE(L1,L2)=LE(length_lb(L1),length_lb(L2))
nlb_FACT(nil_lb)=cons_lb(TRUE,nil_lb)
nlb_FACT(cons_lb(P1,L1))=nlb_MULT(cons_lb(P1,L1),nlb_FACT(L1))
nlb_EXP(L1,nil_lb) = nlb_SUC(nil_lb)
nlb_EXP(L1,cons_lb(P3,L2)) = nlb_MULT(nlb_EXP(L1,L2),L1)
nlb_EVEN(L1)= EVEN(length_lb(L1))
nlb_ODD(L1)=ODD(length_lb(L1))
nlb_DIV(N1,N2) = if nlb_ISZERO(N2)
then ERROR
else if nlb_GE(N1,N2)
then nlb_SUC(nlb_DIV(nlb_SUBS(N1,N2),N2))
else nlb_ZERO
fi
fi
nlb_MOD(N1,N2) = if nlb_ISZERO(N2)
then ERROR
else if nlb_GE(N1,N2)
then nlb_MOD(nlb_SUBS(N1,N2),N2)
else N1
fi
fi
nlb_DIVIDES(L1,L2)=nlb_ISZERO(nlb_MOD(L1,L2))
nlb_SUBS(N1,nil_lb) = N1
nlb_SUBS(N1,cons_lb(P3,N2)) = nlb_PRED(nlb_SUBS(N1,N2))
nlb_EQ_NAT(L1,L2)=EQ_NAT(length_lb(L1),length_lb(L2))
For this case of the 45 axioms in the ADT NAT, 40
can be proved by the ManTa theorem prover. One of the unproved conjectures
shows a real problem (that in this example we will ignore):
nlb_PRED(nlb_ZERO) = nlb_ZEROThis conjecture is proposed since PRED(ZERO)=ZERO in the NAT specification, but after rewriting this expression it becomes
Composition of representations. With the two previous examples a third representation can be obtained automatically via composition. The new representation is BOOL represented with a List of BOOL , that here we call blb.
ADT blb [ ]
/* blb : BOOL -> lb */INITIALS
CONSTRUCTORS
SELECTORS
blb_TRUE : -> lb
blb_FALSE : -> lb
blb_AND : lb * lb -> lb
blb_OR : lb * lb -> lb
blb_NOT : lb -> lb
blb_IMP : lb * lb -> lb
blb_EQ_BOOL : lb * lb -> BOOLAXIOMS
blb_TRUE = nlb_SUC(nlb_ZERO)
blb_FALSE = nlb_ZEROblb_AND(N1,N2) = nlb_MULT(N1,N2)
blb_OR(N1,N2) = if LT(length_lb(concat_lb(N1,N2)),length_lb(nlb_SUC(nlb_ZERO)))
then nlb_ADD(N1,N2)
else nlb_SUC(nlb_ZERO)
fi
blb_NOT(N1) = if nlb_ISZERO(nlb_SUC(nlb_SUC(nlb_ZERO)))
then ERROR
else if nlb_GE(nlb_SUC(N1),nlb_SUC(nlb_SUC(nlb_ZERO)))
then nlb_MOD(nlb_SUBS(nlb_SUC(N1),nlb_SUC(nlb_SUC(nlb_ZE$ else nlb_SUC(N1)
fi
fiblb_IMP(N1,N 2) = blb_OR(blb_NOT(N1),N2)
blb_EQ_BOOL(N1,N2) = EQ_NAT(length_lb(N1),length_lb(N2))
The operations that can be done with the interfaces are:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
To browse and edit proved conjectures |
|
|
|
|
|
|
|
|
|
Although the ERROR symbol could be used inside an expression that is intended to be rewritten, it is not meaningful for the rewriting motor, since ERROR is used only to express where a function is undefined (that is in the axioms of an ADT). When an evaluation includes the ERROR symbol the result is undefined (the only exception is if-then-else-fi that can have one of its second or third expressions undefined an however it can be defined). In terms of programming languages the apparition of ERROR is like an exception or a failed assertion. (Since a function was evaluated in a point of its domain where it was undefined).
With regard to the EQUAL function, it will be rewritten to a EQ_TAD function in accordance to the type. Note that this makes sense since every ADT must have an equality function (the exceptions are extensions, but as it was already discussed these are not ADTs).s
The evaluations of the rewriting Motor always use the axioms given by the user in all the defined ADTs and the following rules:
if TRUE then E1 else
E2
fi -> E1
if FALSE then E1 else E2
fi -> E2
Below, some examples will be given. These examples use the axioms of the ADTs NAT, BOOL and List given in the Appendix A:
FACT(SUC(SUC(SUC(ZERO)))) = SUC(SUC(SUC(SUC(SUC(SUC(ZERO))))))
LT(EXP(SUC(SUC(ZERO)),SUC(SUC(ZERO))),FACT(SUC(SUC(ZERO)))) = FALSE
length(cons(x,nil)) = SUC(ZERO)
Note that in the last example length is applied to a variable x.
This cannot be done in many programming languages, and it is possible due
to the rewriting motor:
MAX(SUC(SUC(X)),SUC(SUC(SUC(X)))) = SUC(SUC(MAX(X,SUC(X))))
MULT(SUC(ZERO),x) = x
ADD(X,Y)=ADD(Y,X)This property although trivial for the user is not trivial for ManTa, since the definition of the function ADD in the ADT NAT doesn't involve explicitly conmutativity:
ADD(N1,ZERO) = N1
ADD(N1,SUC(N2)) = SUC(ADD(N1,N2))
The current theorem prover has to make induction twice in order to prove
this. The proof that it gives is:
Beginning of inductionTo prove a conjecture ManTa tries several techniques:Base case
Substitution: X -> ZERO
ADD(ZERO,Y) = ADD(Y,ZERO)Rule to left side: ADD(ZERO,X) = X
Rule to right side: ADD(N1,ZERO) = N1
Y = YBase case proof successful
Induction step
Induction hypothesis : ADD(_X,Y) = ADD(Y,_X)
Substitution: X -> SUC(_X)
ADD(SUC(_X),Y) = ADD(Y,SUC(_X))Rule to right side: ADD(N1,SUC(N2)) = SUC(ADD(N1,N2))
ADD(SUC(_X),Y) = SUC(ADD(Y,_X))Beginning of induction
Base case
Substitution: Y -> ZERO
ADD(SUC(_X),ZERO) = SUC(ADD(ZERO,_X))Rule to left side: ADD(N1,ZERO) = N1
Rule to right side: ADD(ZERO,X) = X
SUC(_X) = SUC(_X)Base case proof successful
Induction step
Induction hypothesis : ADD(SUC(_X),_Y) = SUC(ADD(_Y,_X))
Substitution: Y -> SUC(_Y)
ADD(SUC(_X),SUC(_Y)) = SUC(ADD(SUC(_Y),_X))Rule to left side: ADD(N1,SUC(N2)) = SUC(ADD(N1,N2))
SUC(ADD(SUC(_X),_Y)) = SUC(ADD(SUC(_Y),_X))Rule to left side: ADD(SUC(_X),_Y) = SUC(ADD(_Y,_X))
SUC(SUC(ADD(_Y,_X))) = SUC(ADD(SUC(_Y),_X))Semantic proof
EQ_NAT(SUC(SUC(ADD(_Y,_X))),SUC(ADD(SUC(_Y),_X))) = TRUERule to left side: EQ_NAT(SUC(N1),SUC(N2)) = EQ_NAT(N1,N2)
EQ_NAT(SUC(ADD(_Y,_X)),ADD(SUC(_Y),_X)) = TRUESemantic proof failed
Induction step proof failedInduction step
Induction hypothesis : SUC(ADD(_Y,_X)) = ADD(SUC(_X),_Y)
Substitution: Y -> SUC(_Y)
ADD(SUC(_X),SUC(_Y)) = SUC(ADD(SUC(_Y),_X))Rule to left side: ADD(N1,SUC(N2)) = SUC(ADD(N1,N2))
SUC(ADD(SUC(_X),_Y)) = SUC(ADD(SUC(_Y),_X))Semantic proof
EQ_NAT(SUC(ADD(SUC(_X),_Y)),SUC(ADD(SUC(_Y),_X))) = TRUERule to left side: EQ_NAT(SUC(N1),SUC(N2)) = EQ_NAT(N1,N2)
EQ_NAT(ADD(SUC(_X),_Y),ADD(SUC(_Y),_X)) = TRUESemantic proof failed
Induction step proof failedEnd of induction
Induction step proof failed
Induction step
Induction hypothesis : ADD(Y,_X) = ADD(_X,Y)
Substitution: X -> SUC(_X)
ADD(SUC(_X),Y) = ADD(Y,SUC(_X))Rule to right side: ADD(N1,SUC(N2)) = SUC(ADD(N1,N2))
ADD(SUC(_X),Y) = SUC(ADD(Y,_X))Rule to right side: ADD(Y,_X) = ADD(_X,Y)
ADD(SUC(_X),Y) = SUC(ADD(_X,Y))Beginning of induction
Base case
Substitution: Y -> ZERO
ADD(SUC(_X),ZERO) = SUC(ADD(_X,ZERO))Rule to left side: ADD(N1,ZERO) = N1
Rule to right side: ADD(N1,ZERO) = N1
SUC(_X) = SUC(_X)Base case proof successful
Induction step
Induction hypothesis : ADD(SUC(_X),_Y) = SUC(ADD(_X,_Y))
Substitution: Y -> SUC(_Y)
ADD(SUC(_X),SUC(_Y)) = SUC(ADD(_X,SUC(_Y)))Rule to left side: ADD(N1,SUC(N2)) = SUC(ADD(N1,N2))
Rule to right side: ADD(N1,SUC(N2)) = SUC(ADD(N1,N2))
SUC(ADD(SUC(_X),_Y)) = SUC(SUC(ADD(_X,_Y)))Rule to left side: ADD(SUC(_X),_Y) = SUC(ADD(_X,_Y))
SUC(SUC(ADD(_X,_Y))) = SUC(SUC(ADD(_X,_Y)))Induction step proof successful
End of induction
Induction step proof successful
End of induction
Successful proof
The current theorem prover of ManTa is not very powerful (6.3% of
proof capacity in NQTHM92 benchmark), there are other inductive theorem
provers that give better results, however this tool is useful for some
rutinary and simple proofs. Before blaming the theorem prover when
it cannot complete a proof, note that it is not possible to make an automatic
theorem prover for interesting theories (like NAT), since
determining the validity of a theorem in such a theory is an indecidible
problem. Writing a theorem prover is hard, in the moment of this writing
the best theorems provers can not prove the correctness of a sort algorithm
neither many other "simple" algorithms.
Developing software with ManTa is not difficult, it is more difficult
to decide what to prove. Usually the modeled ADTs have very interesting
properties that are not evident. For example the function concat
in
the ADT List is not conmutative, but it is associative.
The proof requires induction and can be done in ManTa (i.e concat(concat(x,y),z)=concat(x,concat(y,z))
).
To check what to prove, one way is trying to see algebraic properties
of an ADT (for example conmutativity, associativity, identity, etc.) and
prove or refute them. Another way is checking simple properties that
a correct implementation of a selector must have. For example in
the case of concat and length one property
that they must have is:
length(concat(x,y))=length(x)+length(y)Fortunately, this also can be proved by ManTa after several induction attempts. Decide what to prove is not easy it requires skills, however testing a program also requires skills, and in some ways the theorem prover of ManTa replaces many test cases of a concrete program. (For example in the implementation of the ADT List in C, testing the given property requires a lot of effort).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
All the files that can be generated for an ADT X are:
In the test program, the main operations that can be done with the set
of expressions are: (1) Saving (2) Loading (3) Deleting. In addition
the selectors can be applied to existing expressions to produce new expressions.
ADT BOOL [ ] INITIALS TRUE : -> BOOL FALSE : -> BOOL CONSTRUCTORS SELECTORS AND (c): BOOL * BOOL(i) -> BOOL OR (c): BOOL * BOOL(i) -> BOOL NOT (c): BOOL(i) -> BOOL IMP (c): BOOL(i) * BOOL(i) -> BOOL EQ_BOOL (c): BOOL(i) * BOOL(i) -> BOOL AXIOMS AND(B1,TRUE) = B1 AND(B1,FALSE) = FALSE OR(B1,TRUE) = TRUE OR(B1,FALSE) = B1 NOT(TRUE) = FALSE NOT(FALSE) = TRUE IMP(TRUE,TRUE) = TRUE IMP(TRUE,FALSE) = FALSE IMP(FALSE,TRUE) = TRUE IMP(FALSE,FALSE) = TRUE EQ_BOOL(TRUE,TRUE) = TRUE EQ_BOOL(TRUE,FALSE) = FALSE EQ_BOOL(FALSE,TRUE) = FALSE EQ_BOOL(FALSE,FALSE) = TRUE
ADT NAT [ ]INITIALS
ZERO : -> NATCONSTRUCTORS
SUC : NAT -> NATSELECTORS
ADD : NAT * NAT(i) -> NAT
ISZERO : NAT(i) -> BOOL
MULT : NAT(i) * NAT -> NAT
PRED : NAT(i) -> NAT
MAX : NAT(i) * NAT(i) -> NAT
MIN : NAT(i) * NAT(i) -> NAT
GT : NAT(i) * NAT(i) -> BOOL
LT : NAT(i) * NAT(i) -> BOOL
GE : NAT * NAT -> BOOL
LE : NAT * NAT -> BOOL
FACT : NAT(i) -> NAT
EXP : NAT * NAT(i) -> NAT
EVEN : NAT(i) -> BOOL
ODD : NAT(i) -> BOOL
DIV : NAT * NAT -> NAT
MOD : NAT * NAT -> NAT
DIVIDES : NAT * NAT -> BOOL
SUBS : NAT * NAT(i) -> NAT
EQ_NAT (c): NAT(i) * NAT(i) -> BOOLAXIOMS
ADD(N1,ZERO) = N1
ADD(N1,SUC(N2)) = SUC(ADD(N1,N2))ISZERO(ZERO) = TRUE
ISZERO(SUC(N1)) = FALSEMULT(ZERO,N1) = ZERO
MULT(SUC(N1),N2) = ADD(MULT(N1,N2),N2)PRED(ZERO) = ZERO
PRED(SUC(N1)) = N1MAX(ZERO,ZERO) = ZERO
MAX(ZERO,SUC(N1)) = SUC(N1)
MAX(SUC(N1),ZERO) = SUC(N1)
MAX(SUC(N1),SUC(N2)) = SUC(MAX(N1,N2))MIN(ZERO,ZERO) = ZERO
MIN(ZERO,SUC(N1)) = ZERO
MIN(SUC(N1),ZERO) = ZERO
MIN(SUC(N1),SUC(N2)) = SUC(MIN(N1,N2))GT(ZERO,ZERO) = FALSE
GT(ZERO,SUC(N1)) = FALSE
GT(SUC(N1),ZERO) = TRUE
GT(SUC(N1),SUC(N2)) = GT(N1,N2)LT(ZERO,ZERO) = FALSE
LT(ZERO,SUC(N1)) = TRUE
LT(SUC(N1),ZERO) = FALSE
LT(SUC(N1),SUC(N2)) = LT(N1,N2)GE(N1,N2) = OR(EQ_NAT(N1,N2),GT(N1,N2))
LE(N1,N2) = OR(EQ_NAT(N1,N2),LT(N1,N2))
FACT(ZERO) = SUC(ZERO)
FACT(SUC(N1)) = MULT(SUC(N1),FACT(N1))EXP(N1,ZERO) = SUC(ZERO)
EXP(N1,SUC(N2)) = MULT(EXP(N1,N2),N1)EVEN(ZERO) = TRUE
EVEN(SUC(ZERO)) = FALSE
EVEN(SUC(SUC(N1))) = EVEN(N1)ODD(ZERO) = FALSE
ODD(SUC(ZERO)) = TRUE
ODD(SUC(SUC(N1))) = ODD(N1)DIV(N1,N2) = if ISZERO(N2)
then ERROR
else if GE(N1,N2)
then SUC(DIV(SUBS(N1,N2),N2))
else ZERO
fi
fiMOD(N1,N2) = if ISZERO(N2)
then ERROR
else if GE(N1,N2)
then MOD(SUBS(N1,N2),N2)
else N1
fi
fiDIVIDES(N1,N2) = ISZERO(MOD(N2,N1))
SUBS(N1,ZERO) = N1
SUBS(N1,SUC(N2)) = PRED(SUBS(N1,N2))EQ_NAT(ZERO,ZERO) = TRUE
EQ_NAT(ZERO,SUC(N1)) = FALSE
EQ_NAT(SUC(N1),ZERO) = FALSE
EQ_NAT(SUC(N1),SUC(N2)) = EQ_NAT(N1,N2)
ADT List [ X ]INITIALS
nil : -> ListCONSTRUCTORS
cons : X * List -> ListSELECTORS
head : List(i) -> X
tail : List(i) -> List
length : List(i) -> NAT
concat : List(i) * List -> List
memberList : List(i) * X -> BOOL
isEmptyList : List(i) -> BOOL
EQ_List (c): List(i) * List(i) -> BOOLAXIOMS
head(nil) = ERROR
head(cons(X1,L2)) = X1tail(nil) = ERROR
tail(cons(X1,L2)) = L2length(nil) = ZERO
length(cons(X1,L2)) = SUC(length(L2))concat(nil,L1) = L1
concat(cons(X1,L2),L3) = cons(X1,concat(L2,L3))memberList(nil,X1) = FALSE
memberList(cons(X1,L2),X3) = if EQUAL(X1,X3)
then TRUE
else memberList(L2,X3)
fiisEmptyList(nil) = TRUE
isEmptyList(cons(X1,L2)) = FALSEEQ_List(nil,nil) = TRUE
EQ_List(nil,cons(X1,L2)) = FALSE
EQ_List(cons(X1,L2),nil) = FALSE
EQ_List(cons(X1,L2),cons(X3,L4)) = AND(EQUAL(X1,X3),EQ_List(L2,L4))